Complement of Binary Number
There are two stage of complement:
– One’s complement / 1’s complement
– Two’s complement / 2’s complement
How to get 1’s complement?
To get 1’s complement, we need to invert each bit in binary numbers.
Means that we need to change all 0 to 1 and all 1 to 0.
For
example,
By using 8 bits system,
Binary number = 1001 1110
1’s complement = 0110 0001
How to get 2’s complement?
To get 2’s complement, we just need to add +1 to the 1’s complement.
For example,
By using 8 bits system,
Binary number = 1001 1110
1’s complement = 0110 0001
2’s complement = 0110 0010
Most Significant Bit (MSB)
MSB or sign bits are the first
bit from left.
Based on MSB, we can distinguish the positive and negative numbers.
Based on MSB, we can distinguish the positive and negative numbers.
If the MSB
is 0, then the number is positive.
If the MSB is 1, then the number is negative.
If the MSB is 1, then the number is negative.
The others remaining bits are known as magnitude numbers.
While the least significant bit (LSB) is the right-most bit.
While the least significant bit (LSB) is the right-most bit.
Converting Negative Binary Numbers to Decimal
Now, we will learn how to convert signed negative binary numbers
to decimal.
Check the sign bit first before we do the conversion.
Check the sign bit first before we do the conversion.
Remember: if MSB is 0, the number is positive else if the MSB is
1, the number is negative.
Example 1
By using 4 bit system, convert 1011 to decimal number.
By using 4 bit system, convert 1011 to decimal number.
Step 1: check the MSB
Binary number = 1011
MSB = 1, it is a negative number.
Binary number = 1011
MSB = 1, it is a negative number.
Step 2: convert to decimal
Adding the value in bottom row:
– 8 + 2 + 1 = – 5
Hence, the decimal number
is – 5
Example
2
By using 8 bit system, convert
1111 0110 to
decimal number.
Step 1: check the MSB
Binary number = 1111 0110
MSB = 1, it is a negative number.
Binary number = 1111 0110
MSB = 1, it is a negative number.
Step 2: convert to decimal
Adding the value in bottom row:
– 128 + 64 + 32 + 16 + 4 + 2 = – 10
Hence, the decimal number
is – 10
Example 3
By using 8 bit system, convert
0110 0011 to
decimal number.
Step 1: check the MSB
Binary number = 0110 0011
MSB = 0, it is a positive number.
Binary number = 0110 0011
MSB = 0, it is a positive number.
Step 2: convert to decimal
Adding the value in bottom row :
64 + 32 + 2 + 1 = 99
Hence, the decimal number is 99.
Examples of Calculation
Example 1:
By using 8 bit system, show how computer use binary to calculate 9 + 10.
Step 1: Convert decimal number to binary number.
9 — 0000
1001
10 — 0000
1010
Step
2: Calculation
Example 2:
By using 8 bit system, show how computer use binary to calculate 14 – 5.
We can do 14 – 5 by using addition, that is 14 + (-5).
We can do 14 – 5 by using addition, that is 14 + (-5).
Step 1: Convert 14 to binary number.
14 — 0000 1110
Step 2: Convert – 5 to 2’s complement.
5 — 0000 0101
1’s complement — 1111 1010 (invert each bit)
2’s complement — 1111 1011 (adding +1)
-5 — 1111 1011
5 — 0000 0101
1’s complement — 1111 1010 (invert each bit)
2’s complement — 1111 1011 (adding +1)
-5 — 1111 1011
Step 3: Calculation
This is dummy text. It is not meant to be read. Accordingly, it is difficult to figure out when to end it. But then, this is dummy text. It is not meant to be read. Period.
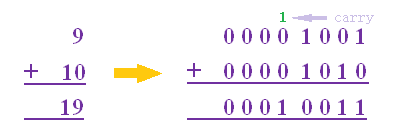
ConversionConversion EmoticonEmoticon